The purpose of this project, launched on Sep 25, 2024, is to explore the space of equational theories of magmas, ordered by implication. To begin with we shall focus only on theories of a single equation, and specifically on the 4694 equational laws involving at most four magma operations, up to symmetry and relabeling (here is the list in Lean and in plain text). This creates 4694*(4694-1) = 22,028,942 implications that need to be proven or disproven, creating both “implications” and “anti-implications”.

We will accumulate both “proven” and “conjectured” implications and anti-implications: proven assertions will be verified in the proof assistant language Lean, and “conjectured” assertions represent all claims (either human-generated or computer-generated) that have not yet been verified in Lean. The current status of the project can be found on the dashboard.

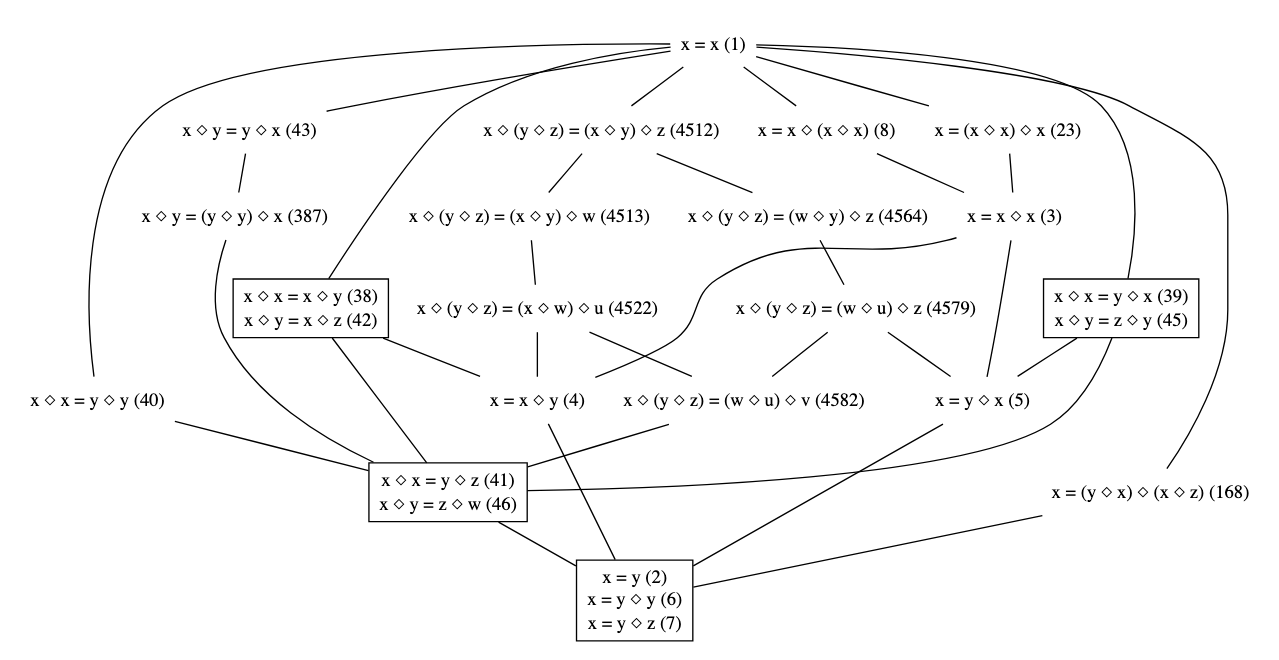
Some selected equations of interest are listed here (in Lean form) and here (in a human readable blueprint). Examples include

• Equation 1: x = x. The trivial law.
• Equation 2: x = y. The singleton law.
• Equation 43: x ◇ y = y ◇ x. The commutative law.
• Equation 46: x ◇ y = z ◇ w. The constant law.
• Equation 4512: x ◇ (y ◇ z) = (x ◇ y) ◇ z. The associative law.

Here is a tour of several selected equations, including the ones above.

Current statistics and data files, updated automatically:

• dashboard

Current visualizations, updated automatically:

• Equation Explorer is a tool for exploring the graph of equation implications.
• Finite Magma Explorer is a tool for exploring finite magmas and the equations they satisfy.
• Graphiti is a tool for visualizing the implication graph.

For guidelines on how to contribute, see the CONTRIBUTING.md file. Participants are requested to abide by our code of conduct.

Building the project

To build this project after installing Lean and cloning this repository, follow these steps:

% cd equational_theories/
% lake exe cache get
% lake build

Links

• Main web page
  • Blueprint
  • Documentation
  • The Lean Zulip stream for the project
  • Instructions on how to contribute
  • Code of conduct
  • Wiki
  • Older progress
• A blog post describing the project., Sep 25, 2024.
  • The equational theories project: a brief tour, Oct 12, 2024 - a followup to the previous post.
• Initial discussion on Zulip, Sep 26, 2024.
• Initial discussion on Mastodon, Jul 18, 2023.
  • Followup discussion on Mastodon, Sep 25, 2024.
• The MathOverflow post that inspired the project, Jul 17, 2023.
  • A related MathOverflow post, Jul 16, 2023.
• Data
  • Text list of equations. Larger list with equations of up to five operations
  • List of duals of equations (JSON)
  • The smallest magma obeying a given equation (up to N=5), if it exists (and the magmas themselves)
  • To download the current state of the implication graph, see this thread.
• Scripts
  • Shell
    • run_before_push - performs some of the CI checks, suitable for running just before pushing a new PR
  • Lean
    • extract_implications - extracts implications from one or more Lean files. This outputs the “ground truth” of implication data, for use by other scripts
  • Python
    • explore_magma - test a given magma table against all or a subset of the equations in Equations/All.lean
    • find_dual - finds the dual of an equation
    • find_equation_id - finds the equation number of an equation string
    • find_powerful_theorems.py - finds theorems that, if proved, would imply many others
    • generate_eqs_list - generates a list of equations
    • generate_image - generates an image of implications
    • generate_most_wanted_list - generates the “most wanted” implications
    • generate_z3_counterexample - given an implication statement between two equations, calls Z3 to try to generate a counterexample
    • process_implications - processes implications from one or more Lean files
  • Ruby
    • generate_graphviz_graph - creates a graphviz graph
    • transitive_closure - computes the transitive closure of a set of implications
    • transitive_reduction - finds a transitive reduction of a set of implications
    • graph - graph library
• Automated provers for equational theories
  • Prover9 and Mace4
    • aa - a project to use Prover9/Mace4 to brute force axioms for finite mathematical domains
  • Vampire
  • eprover
  • twee
  • zipperposition
  • Z3
  • Knuckledragger
  • A blog post by Philip Zucker testing many of the above provers on a sample implication of this project.
  • “Guided Equality Saturation”, Thomas Kœhler, Andrés Goens, Siddharth Bhat, Tobias Grosser, Phil Trinder, Michel Steuwer, Jan 5, 2024.
  • “Rewrite Rule Inference Using Equality Saturation”, Chandrakana Nandi, Max Willsey, Amy Zhu, Yisu Remy Wang, Brett Saiki, Adam Anderson, Adriana Schulz, Dan Grossman, Zachary Tatlock, 23 Aug, 2021.
• Other tools
  • egg - e-graphs good
  • MiniZinc - high-level constraint modeling language
  • nauty - graph automorphism tool
  • KBCV - Knuth-Bendix completion visualizer
  • Instagraph - knowledge graph generator
  • Logic Programming in F# - Code and Examples from John Harrison’s “Handbook of Practical Logic and Automated Reasoning”, translated to F#
    • Original code, written in OCaml
    • Validated Knuth-Bendix code, written in OCaml
• Blog posts and media mentioning this project
  • “We’re Entering Uncharted Territory for Math”, Matteo Wong, The Atlantic, Oct 4 2024.
  • “On Math Platform”, Michael Bucko, Substack von Michael, Oct 5 2024.